When a machine learning model is deployed in production, the main concern of data scientists is the model pertinence over time. Is the model still capturing the pattern of new incoming data, and is it still performing as well as during its design phase?

Monitoring model performance drift is a crucial step in production ML; however, in practice, it proves challenging for many reasons, one of which is the delay in retrieving the labels of new data. Without ground truth labels, drift detection techniques based on the model’s accuracy are off the table.
In this article, we will take a brief but deep dive into the underlying logic behind drift as well as present a real-life use case with different scenarios that can cause models and data to drift.
Measuring Data Drift: A Practical Example
Let’s say we want to predict the quality of the Bordeaux bottles at the wine shop near our place. This will help us save some money (and avoid some not-worth-it hangovers).
To do this, we will use the UCI Wine Quality dataset as training data, which contains information about red and white variants of the Portuguese “Vinho Verde” along with a quality score varying between 0 and 10.
The following features are provided for each wine: type, fixed acidity, volatile acidity, citric acid, residual sugar, chlorides, free sulfur dioxide, total sulfur dioxide, density, pH, sulphates, and alcohol rate.
To simplify the modeling problem, let’s say that a good wine is one with a quality score equal to or greater than 7. The goal is thus to build a binary model that predicts this label from the wine’s attributes.
For purposes of demonstrating data drift, we explicitly split the original dataset into two:
- The first one contains all wines with an alcohol rate above 11%, wine_alcohol_above_11.
- The second one contains those with an alcohol rate below 11%, wine_alcohol_below_11.
Such clear differences between the two datasets will be formalized as data drift. We split wine_alcohol_above_11 to train and score our model, and the second dataset wine_alcohol_below_11 will be considered as new incoming data that needs to be scored once the model has been deployed.
At this point, you would naturally expect a discrepancy between the scores. Why is that? Because clearly — as you’ll see in the next section — this violates the underlying IID assumption.
A Small Detour Through Statistical Learning
Let’s consider a classical supervised learning task with training set S = {(xᵢ, yᵢ)}, with xᵢ ∈ X and yᵢ ∈ Y, and a risk function r: YxY→ R. We wish to learn a predictive function f : X → Y that not only minimizes the empirical risk (on the set S) but also the generalization risk (on unseen data). Under the statistical learning framework, the generalization risk can be faithfully estimated from the empirical risk. This PAC theorem uses Hoeffding’s inequality, which relies on the infamous Independent and Identically Distributed (IID) assumption.

Under this assumption, each pair of observations (x, y) is drawn independently from the same joint distribution p(X,Y). Intuitively, this means that the training set S is a reasonable protocol through which we can get partial information about the underlying true function f.
If the above assumption does not hold, the empirical risk on the training set is no longer a robust estimation of the expected empirical risk on new unseen data. In other words, the test error is no longer a good estimation of future errors.
With that, we will now investigate different scenarios where this assumption fails and causes data drift.
What Is Data Drift?
In the literature, several terms and formulations are used to describe the problem of data drift, here we employ the framework presented by Quiñonero Candela.

This is a violation of the IID assumption presented in the first section.
For a causal task, the joint distribution can be appropriately decomposed as: P(x,y) = P(x)P(y|x), thus a change in P(x,y) can come from a change of these two distributions. Similarly for anti-causal tasks where the appropriate decomposition is P(x,y) = P(y)P(x|y).
Before discussing the possible drift situations, let’s present two frequent root causes for this.
Some Examples Causes of Data Drift
Sample selection bias: Training sample is not representative of the population.
For instance, building a model to assess the effectiveness of a discount program will be biased if the best discounts are proposed to the best clients. Selection bias often stems from the data collection pipeline itself.
In our wine example, the original dataset sample with alcohol level above 11 degrees surely does not represent the whole population of wines — this is sample selection at its best.
Non-stationary environment: Training data collected from source population does not represent the target population.
This often happens for time-dependent tasks — such as forecasting use cases — with strong seasonality effects. Learning a model over a given month won’t generalize to another month.
Back to wine again: one can imagine a case where the original dataset sample only includes wines from a specific year, which might represent a particularly good (or bad) vintage. A model trained on this data may not generalize to other years.
Back to Our Example…
To keep the problem simple, we employ a univariate point of view, focusing on the feature alcohol. However, the reasoning can be generalized to multiple dimensions, which is usually the case in practice (several features drifting at the same time).
The question we want to address here is:
Will the performance of a model trained on my training set (wines with an alcohol level above 11%) change drastically when scoring new bottles (whose alcohol level is below 11%)?
One important detail to note is that the assessment is about the comparative performance of the model between original and new data, and not about the absolute performance of the model.
If we have the ground truth labels of the new data, one straightforward approach is to score the new dataset and then compare the performance metrics between the original training set and the new dataset. However, in real life, acquiring ground truth labels for new datasets is usually delayed. In our case, we would have to buy and drink all the bottles available, which is a tempting choice… but probably not a wise one.
Therefore, in order to be able to react in a timely manner, we will need to base performance solely on the features of the incoming data. The logic is that if the data distribution diverges between the training phase and testing phase, it is a strong signal that the model’s performance won’t be the same.
With that being said, the question above can be answered by checking data drift between the original training set and the incoming test set.
The Drift Zoology
Now let’s get back to our wines and take a closer look at different situations where data drift occurs. Throughout this section, this is how our model is trained and originally tested.
From the wine_alcohol_above_11 dataset, we randomly split them into two:
- The first one to train the model, denoted by alcohol_above_11_train, will be further split in training and validation sets.
- The other one for testing the model called alcohol_above_11_test.
We fit a Random Forest model on alcohol_above_11_train. The model achieves a F1 Score of 0.709 on the hold-out set.
Situation 1: No Drift
Here the target dataset is the source dataset wine_alcohol_above_11:
The random sampling gives us two datasets with the similar alcohol rate distribution. Based on the IID assumption, the performance of the model should not change much between hold-out data of train set and test set.
When using this model to score the alcohol_above_11_test dataset, the F1 score is 0.694: when there is no drift in alcohol rate distribution between train and test set, there seems to be no drift with other features too, and the relationship learned between the features and the target holds for the test set.
In formal terms, as neither P(x) nor P(y|x) has changed, the model’s performance on the new dataset are similar.
With the trained model above, we take a closer look at the F1 score per alcohol bin on the alcohol_above_11_test dataset:
Two important observations can be drawn from this chart:
- If there are a lot of wines with alcohol levels between 10% and 12% in the new unseen dataset, we should expect the F1 score on these new data to degrade. On the contrary, if more wines between 13% and 14% come in, the performance will be better.
- Until now, the model has only seen alcohol levels between 11% and 14%. If it has to score some wines with alcohol levels out of that range, its performance is unpredictable — it can go either up, or (more probably) down.
Situation 2: Feature Drift (Or Covariate Drift)

With the exception of the final bin, which is still in the usual range, the performance drops dramatically for everything else.

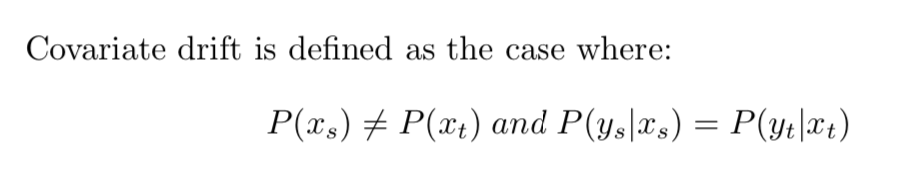
Here’s another illustration of this situation in the literature, where the original training set does not faithfully represent the actual population and thus the model learned from it is biased and does not work well on test data:

In our specific use case, model retraining can definitely improve the performance, as the model will have a chance to learn from wines with alcohol range outside of 11% -14%.
Situation 3: Concept Drift

Situation 4: Dual drift

Conclusion
In theory, there is not a definitive correlation between the degradation of model performance and any types of data drift. That being said, in practice, observing data drift is a red flag about the pertinence of the deployed model, and a model reconstruction step is highly recommended.




