As more open source models are released and begin to rival the quality of proprietary models like ChatGPT, many practitioners want to test out these models for their own use cases.
However, loading even a relatively small model such as Llama2 7B and performing inference requires approximately 30GB of GPU memory. The largest Llama2 model at 70B parameters requires approximately 320GB of GPU memory which can be prohibitive. If we then also wish to fine-tune this model for a specific task, the requirements increase even further.
If instead of loading the model weights at 32-bit precision, they can be reduced down to 8-bit, 4-bit, or an even lower precision, it becomes possible to load and run these models on consumer hardware, democratizing access to LLMs and their applications.

Before we start, this blog is not a tutorial on how to quantize a model. If that is what you are looking for, check out this Hugging Face blog. This blog aims to give a quick introduction to the different quantization techniques you are likely to run into if you want to experiment with already quantized Large Language Models (LLMs). It is the second article in our three-part series that unpacks technical topics that have made their way into the spotlight as a result of the growth and exploration of LLMs.
The Key Challenge Is Retaining Model Performance
Applying quantization to reduce the weights of a neural network down to a lower precision naturally gives rise to a drop in the performance of the model. This is commonly measured as a difference in perplexity between the original and quantized models on a dataset such as wikitext2 [2] which is downstream task agnostic. Perplexity can be thought of as the model’s uncertainty in predicting the next word in a sequence, it is the exponential negative log-likelihood of a sequence of tokens.
Minimizing this drop in performance while compressing an LLM to ever lower precision is a key challenge, and many new techniques have been proposed to reduce performance loss.
Recent techniques such as Sparse-Quantized Representation (SpQR) [3] are now capable of quantizing a model down to approximately four bits per parameter with the difference in perplexity of <1%.

The Basics of Quantization
When reducing the precision of a tensor, the range of values that can be represented will usually drop. For example, when reducing a 32-bit floating point down to an 8-bit integer, for example, the range will be lowered from [-3.4e38, 3.40e38] to [-127, 127]. This means that the tensor will need to be mapped from one range to another and rounded to the nearest value.
This can be illustrated as:
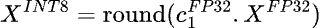
where
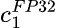
is the quantization constant or scale factor and represents the ratio of the maximum of the smaller range to the absolute maximum value present in the higher precision tensor.
Dividing the parameters by the scale factors will dequantize the parameters. Performing computation on the quantized parameters at inference time usually requires dequantization, thus the scale vectors must be stored.
One issue that arises with this simple approach is that outliers can have a large impact on this scaling, meaning that the full range of the lower precision data type is not effectively used, which degrades the performance of the model.
Introducing Blocks
To address this, a block-wise approach can be used. To create a block, the tensor is flattened and divided into segments of sizes such as 64 or 128, and each segment can then be scaled individually. This limits the impact of these outliers to only certain blocks.
Smaller blocks yield higher accuracy, however the trade-off is that this increases the number of parameters that need to be stored as now there is one scaling factor for every block.
Double Quantization
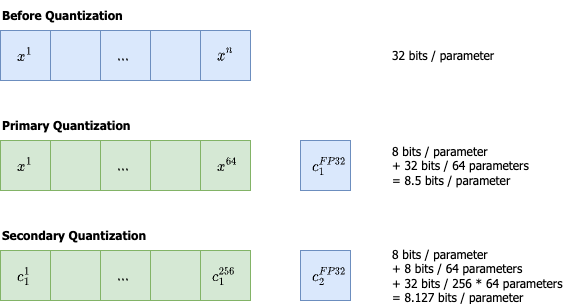
The QLoRA paper [4] offers a solution by proposing Double Quantization. This involves performing a second round of quantization, this time to quantize the scaling factors from the initial quantization of the weights. The 32-bit scale factors are grouped into blocks of 256 and scaled down to 8-bit precision with the introduction of a second round quantization factor.
As illustrated below, storing one scaling factor in 32-bit for every block of 64 parameters adds 0.5 bits per parameter (32/64). Instead, using this double quantization to compress the per block scaling factors to 8-bit results in a reduction to only 0.127 bits per parameter (8/64 + 32/(256*64)).
GPTQ
Another popular technique for quantization is GPTQ [5], which approaches the quantization layer by layer. GPTQ takes in a small calibration dataset. It then solves for the optimal quantized weight matrix for each layer that minimizes the squared error between the outputs of the quantized and full precision layer. Then the individual layers are re-combined. They perform quantization down to 3- and 4-bit precision.
GPTQ has also been integrated into Hugging Face via the AutoGPTQ library.
SpQR
Building upon the observation that outliers in the parameters can have a large negative impact on the compressed model performance, Sparse-Quantized Representation (SpQR) [2] proposes to use a higher precision for the outliers while quantizing the rest of the parameters to 3-bit.
This variable bit rate technique is shown to be nearly lossless at an effective bit rate of <4.75 bits per parameter.
GGML/GGUF
If you have been test driving smaller models on your local machine using frameworks such as llama.cpp, Ollama, or LMStudio you will almost certainly have come across the formats GGML and GGUF.
GGML [6] is the name of the C library written by Georgi Gerganov which produces binary files which are optimized for CPU. The binary file format GGUF is a successor of the GGML format.
This library uses a block-based approach with their own system for further quantizing the quantization scaling factors, known as the k-quant system.
Efficient Fine-Tuning With Quantization: QLoRA
So far, these techniques focus on taking a pretrained model and compressing the parameters to make inference more efficient. But what about when we want to fine-tune a model for a specific task?
Numerous efficient fine-tuning algorithms have been proposed recently, you can read part one of this series for an overview.
Techniques such as LoRA maintain the original weights frozen and add a small set of trainable weights, ofter called adapters, to train during the fine-tuning. These techniques can also benefit from quantization by loading a quantized version of the base model.
QLoRA develops quantization of the parameters down to 4-bit with Double Quantization of the scaling factors down to 8-bit. While this can be used without fine-tuning, they also demonstrate that this 4-bit quantized version can replace the 16-bit base model and LoRa can be used to fine-tune the new parameters at 16-bit.
This brings down the memory requirements to fine-tune a 65B parameter model from ~780GB to <48GB, which makes it achievable on a single GPU machine. QLoRA has been integrated into Hugging Face.
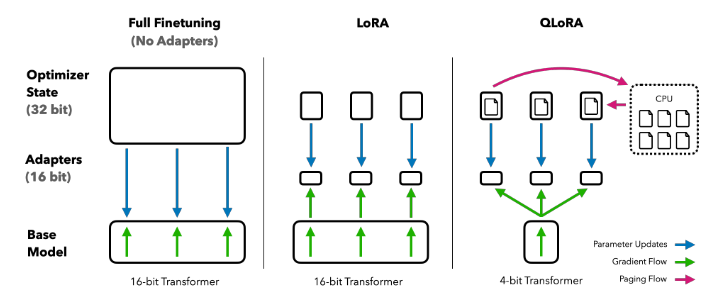
Figure 3: QLoRA uses a 4-bit quantization of the base transformer model to further improve the efficiency of LoRA for fine-tuning. They also introduce a paging mechanism to transfer the optimizer states to CPU during GPU memory spikes to avoid out-of-memory errors and ease the training of large models on a single machine. [4]
How Low Can We Go?
Researchers continue trying to push the envelope and recent work has shown the feasibility of reaching sub-1-bit compression for Mixture of Experts models in particular.
Mixture of Experts models replace dense layers with a collection of sparse experts, each expert being a neural network. They then use a routing system to send input tokens to one of the many experts.
This allows for faster inference time as a token only passes through part of the network but means that memory requirements remain high due to the large parameter counts associated with having many experts. For an introduction to Mixture of Experts models, this blog is comprehensive.
The QMoE framework [7] was able to compress a 1.6 trillion parameter SwitchTransformer model down to only 0.8 bits per parameter with only a small performance degradation.
This is an exciting area to watch as these advancements continue to render ever more powerful open source language models accessible.
References
[2] Stephen Merity, Caiming Xiong, James Bradbury, and Richard Socher. Pointer sentinel mixture models. arXiv preprint arXiv:1609.07843, 2016
[3] Dettmers, T., Svirschevski, R., Egiazarian, V., Kuznedelev, D., Frantar, E., Ashkboos, S., Borzunov, A., Hoefler, T., & Alistarh, D. (2023). SpQR: A Sparse-Quantized Representation for Near-Lossless LLM Weight Compression. http://arxiv.org/abs/2306.03078
[4] Dettmers, T., Pagnoni, A., Holtzman, A., & Zettlemoyer, L. (2023). QLoRA: Efficient Finetuning of Quantized LLMs. http://arxiv.org/abs/2305.14314
[5] Frantar, E., Ashkboos, S., Hoefler, T., & Alistarh, D. (2022). GPTQ: Accurate Post-Training Quantization for Generative Pre-trained Transformers. http://arxiv.org/abs/2210.17323
[6] https://github.com/ggerganov/ggml
[7] Frantar, E., & Alistarh, D. (2023). QMoE: Practical Sub-1-Bit Compression of Trillion-Parameter Models. http://arxiv.org/abs/2310.16795




