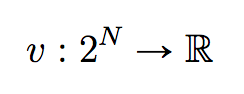It’s no secret that marketing today relies heavily on data analytics and data science. Endless applications have been wildly studied and successfully applied in this regard, ranging from customer segmentation and targeting to building recommender systems and predicting churn.
In this blogpost, we are going to address yet another interesting application of data science in marketing, which is marketing attribution. Unlike the above examples, marketing attribution unfortunately still lacks a rigorous data-driven approach, and it is largely addressed nowadays through rigid business rules.
This blogpost will introduce the subject of marketing attribution and present a novel way to do attribution modeling that uses game theory. The content of this blogpost will be very technical at times. We are going to have a look at some key aspects of the theory behind the models and share some parts of the code when it makes sense. Let’s get started!
The content of this blogpost will be very technical at times. We are going to have a look at some key aspects of the theory behind the models and share some parts of the code when it makes sense. Let’s get started!
What Is Marketing Attribution?
Let’s start with an example!

Suppose you’re running a digital lemonade stand and you are in charge of promoting the product. You come up with the brilliant idea to advertise your lemonade on social media, so you massively invest on this channel. As a precaution, you also choose to make minor investments on other channels: Google Ads, display ads, and a few others.
Now that you have made some profit, you want to know if investing heavily on social media was actually a good move: What percentage of the total profits did the social media channel generate? Does it justify your spending on it? Based on the results, was it reasonable to spend that kind of money on this channel, and should you continue to do so? These are the kind of questions that marketing attribution addresses.
More formally:
Marketing attribution is the process of assigning the credit of a purchase (or any other action of interest, such as subscribing to a newsletter or downloading some content — this is what we call a conversion) to the right marketing channels, given all the channels that the customer interacted with prior to the purchase.
Why is it important ? It is pretty straightforward to see how attributing conversions to the right channels might boost sales and benefit the company. First of all, and most importantly, by optimizing your spending on the right channels, you will naturally improve the ROI, which is the ultimate goal of any marketing strategy. Second, actually knowing which channels drove the conversions simply improves your understanding of the customer journeys and enables you to enhance and adjust your marketing strategy accordingly.
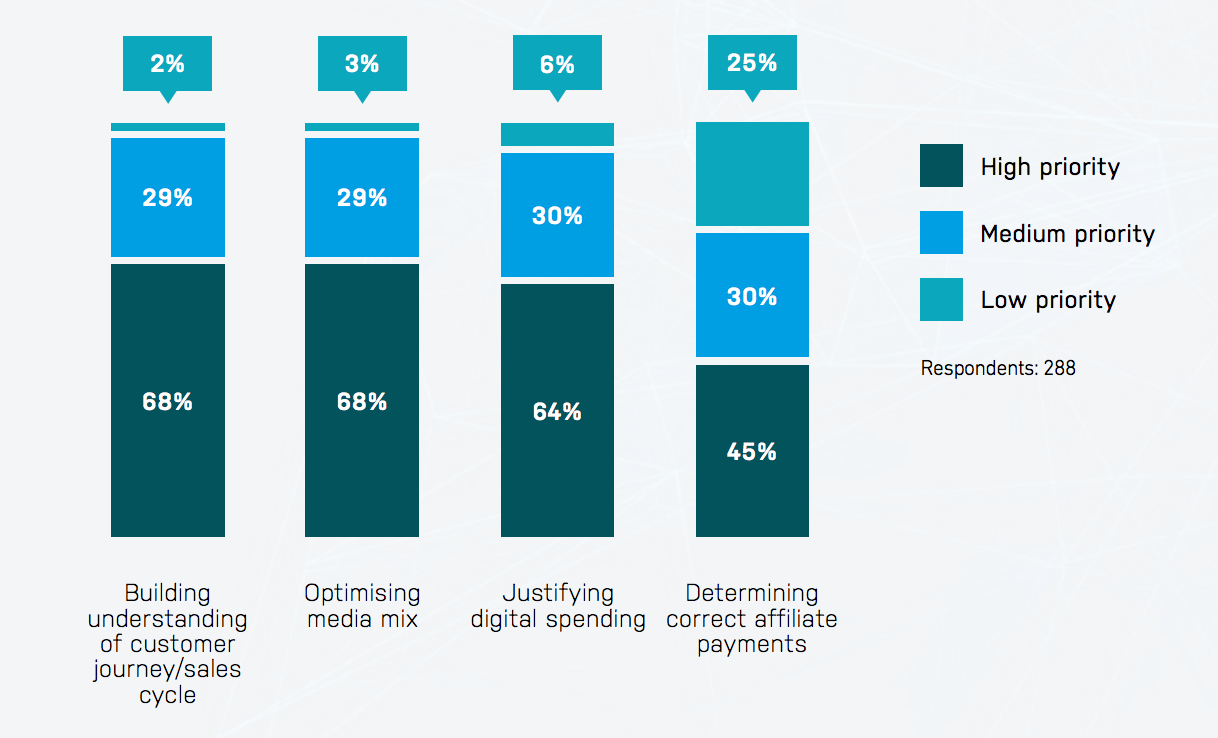
You might ask yourself at this point: Do I even have a marketing attribution problem? The answer is probably yes! In today’s digital world, there’s a vast number of media where the customer could interact with your product (Facebook, twitter, Google Ads, etc.), and more often that not, the customer will interact with more than one of these media before making the decision to buy your product. This makes it notoriously difficult to attribute credit to the right marketing channel and calls for an adequate attribution analysis.
It is safe to say that this problem is not a recent one and that marketing attribution is now a mature field, with most organizations reporting that they already perform some kind of attribution analysis.
Unfortunately, the most widely used techniques today for marketing attribution have some ingrained biases that makes them ineffective. I’m referring here to the so-called heuristic models. We are going to have a look at one of these models, which is perhaps the most known and used model of them all: the last click model:
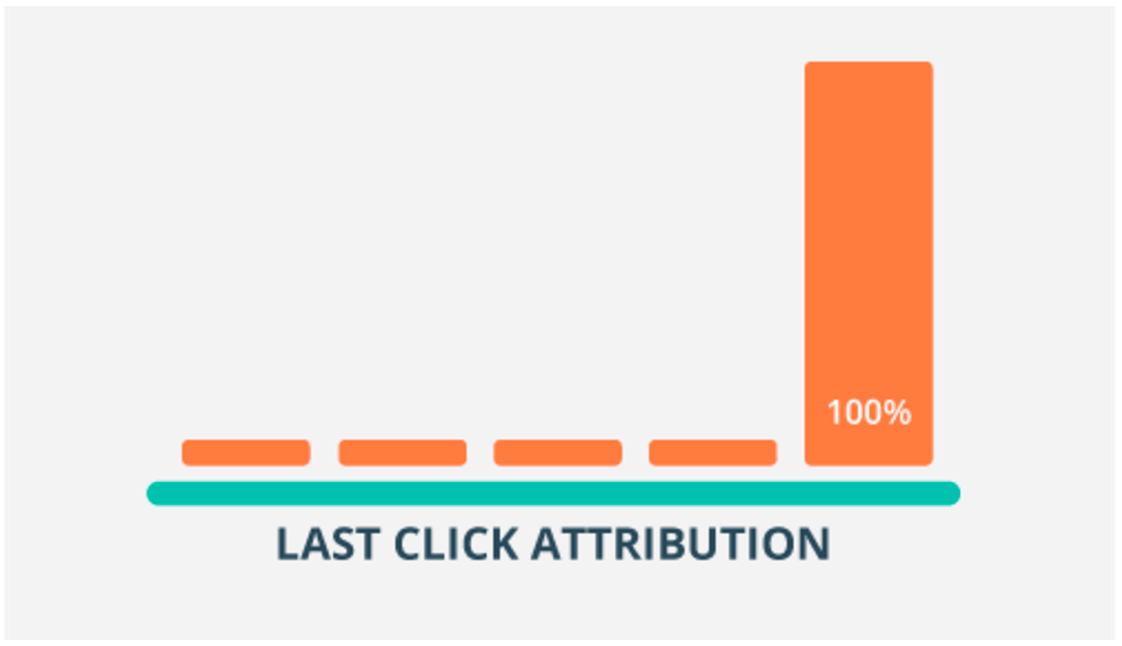
As the name suggests, this model consists of attributing the credit of the purchase entirely to the marketing channel prior to that purchase. If we go back to our digital lemonade stand example, this would mean that we should assign all of the credit for the customer’s purchase to social media. It is not difficult to see that there’s something wrong with this logic. How about the other channels? If it is the case that the remaining channels should get no credit, could we safely discard them and retain all of our conversions? Probably not!
The common main flaw that these models share is the fact that they base the attributions solely on a set of rules (e.g., the last channel should get the credit, all the channels should get equal credit, etc.) rather than exploring the correlation between the channels and the conversion (and using this as a basis for attributing the right amount of credit to each channel).
Enter Algorithmic Attribution
Compared to the heuristic models, this is a fairly new approach to attribution analysis. The idea behind these models is to get rid of the set of rules that drive the heuristic models and instead model the relation that exists between the marketing channels and purchasing an item based on insights that we get from data.
Several models have been proposed based on different mathematical theories: Markov models, game theory models (you can see this or this), Survival Analysis models, etc. In this blog post, we are going to focus on the game theory model. We are going to go through the theoretical parts behind this modelization as well as some technical aspects of its implementation (using SQL and Python).
Game theory is a vast field of mathematics that has been around for many decades but was only formalized in the 1950s by John von Neumann. It has since proved to be a useful tool in many fields and applications, including modeling the competition between firms (economics), voting strategies and peace negotiations between countries (politics), competition between animal species and natural selection (biology), or even choosing the winning strategy to pick up — or not — the blonde girl at the bar (I’m referring to the bar scene from the excellent movie A Beautiful Mind).
More generally, game theory aims to understand situations where rational decision-makers interact (e.g., take actions, threaten each other, and possibly form coalitions). There are two big families of games: non-cooperative games and cooperative games. As their names suggest, the first family deals with situations where players act independently and according to their own incentives. The latter deals with situations where players can agree and form coalitions. For the purpose of attribution modeling, this blog post will focus on cooperative games.
A cooperative game can be defined by a set of players N={1,2,…,n}, and a real valued function v, called the characteristic function, which assigns to each subset A in N, a real value called the worth of A. A is called a coalition, and the worth of a coalition can be viewed as the payoff that it can generate when its members are working together.
Now here comes the fun part: we can actually model the interactions that customers have with marketing channels as a cooperative game. Each marketing channel can be seen as a player in the game, and the set of all players/channels can be though of as working together in order to drive the conversions.
The tricky part lies in defining the right characteristic function. For each coalition of channel, this function should be able to reflect the value (or the payoff) that is created when these channels interact together. Numerous definitions have been suggested and studied in the literature:
- We can define v(A) as being the conditional probability of conversion given A (i.e., given that the user has interacted with all the channels in the coalition A) : P(Conversion|A). This quantity can then be approximated directly from the data by fitting, for example, a predictive model on all the subsets of channels.
- Alternatively, we can define it simply as the total number of conversions that this coalition generated.
We are going to go with the simpler definition and use the following (from Sebastian Cano Berlanga, Cori Vilella, et al. Attribution models and the cooperative game theory):
For every coalition A in N:

C(S) is the total number of conversions generated by the subset of channels S.
This means that the worth of a coalition A is the sum of the conversions that were generated by every subset of channels belonging to A.
Under this definition, the value of the grand coalition (i.e., the coalition containing all the channels) corresponds to the total number of conversions that occurred.
Then the big question is, how can we guarantee a fair attribution of this value (the total number of conversions) among all the channels involved?
The concept of fairness can — and has actually been — axiomatized in a few simple and logical rules. These rules are the following:
- Efficiency: The total allocations of all players must sum to the total payoff (i.e., the conversions attributed to each channel should sum to the total number of conversions).
- Symmetry: Interchangeable players (i.e., players who always contribute with the same amount to every coalition) should receive the same allocations.
- Dummy player: If the contribution of a player to any coalition is always equal to the payoff that he can generates alone, then this player should receive the amount that he can achieve on his own.
- Additivity: Consider two different games A and B with characteristic functions a and b, and a third game C with characteristic function c, such that: c(S) = a(S) + b(S) for every coalition S. Then each player’s payoff in each coalition S under game C, should be the sum of the payoffs he would have generated under the two separate games, A and B.
For any coalitional game (N,v), there exits a unique way of dividing the payoffs among the players, that satisfies axioms one, two, three, and four.
This distribution of payoffs is called the Shapley value:

Interpretation of Marketing Attribution Models
We can interpret this equation in several ways. First of all, the Shapley value of channel i can be seen as the weighted sum of the incremental values that channel i adds to all the coalitions that don’t contain this channel. Another interpretation would be to imagine that we’re forming the grand coalition (i.e., the coalition containing all the players) by entering each player in the coalition one player at a time, and that each player receives the value by which he increases the coalition’s worth. The value that a player receives would then depend on the order in which he joined the coalition. The Shapley value can then be seen as the average of the values that each player receives if the players are entered in a random order.
Let’s walk through a simple example: suppose that we are running a campaign to promote a particular product or service and that we are only using two marketing channels:

Let’s assume that during this campaign, we recorded the following conversions:

- Five customers converted after clicking on a Facebook ad.
- 10 custumers converted after clicking on a sponsored Google search result.
- 30 customers converted only after clicking on both ads.
Let’s apply the above definition of the Shapley value to attribute a proportion of the total number of conversions that happened to each channel (5 + 10 + 30 = 45 conversions happened in total).
We’ll start with the Facebook ad channel. There are only two coalitions that do not contain this channel: The empty coalition S={ø} and the coalition containing the channel Google AdWords S={GoogleAd}. These will constitute the summands of the Shapley equation:

As an example, here is how we computed the value of v({GoogleAd,Facebook}):
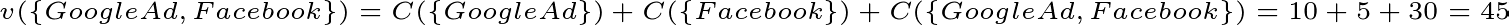
Finally, we need to introduce the weights for each summand. Here are the final results (we applied the same steps for the channel Google AdWords):

Let’s Get Technical!
Let’s get down to preparing the data. We’ll assume we start with a generic table with the following schema as the raw inputs:
user_logs : user_id | channel | timestamp | conversion
- user_id: A unique identifier of each user.
- channel: The marketing channel visited by the user “user_id”.
- timestamp: The time of the visit.
- conversion: A binary variable that is1 if the user converted after visiting “channel” and 0 otherwise.
The user_id can be anything that is able to uniquely identify each customer. If the customer is signed in on the website, then his interactions with the marketing channels can be precisely tracked; if not, cookies are usually used to record these interactions.
As a first step, we need to compute the sum of conversions C(S) that each subset of channels S has yielded. The following SQL query (we are using the Postgres flavor here) does this, and produces a table with the following schema:
subsets_conversions : channels_subset | conversions_sum
SELECT "channels_subset",
sum("conversion") as "conversions_sum"
FROM
(
SELECT "user_id",
string_agg(DISTINCT("channel"), ',') as "channels_subset",
max("conversion") as "conversion"
FROM
(
SELECT "user_id",
"channel",
"conversion"
FROM "MARKETINGATTRIBUTIONSIMULATIONS_simulated_data"
ORDER BY
"user_id",
"channel"
)a
group by "user_id"
)b
GROUP BY "channels_subset"
The first rows of the output could look something like this:
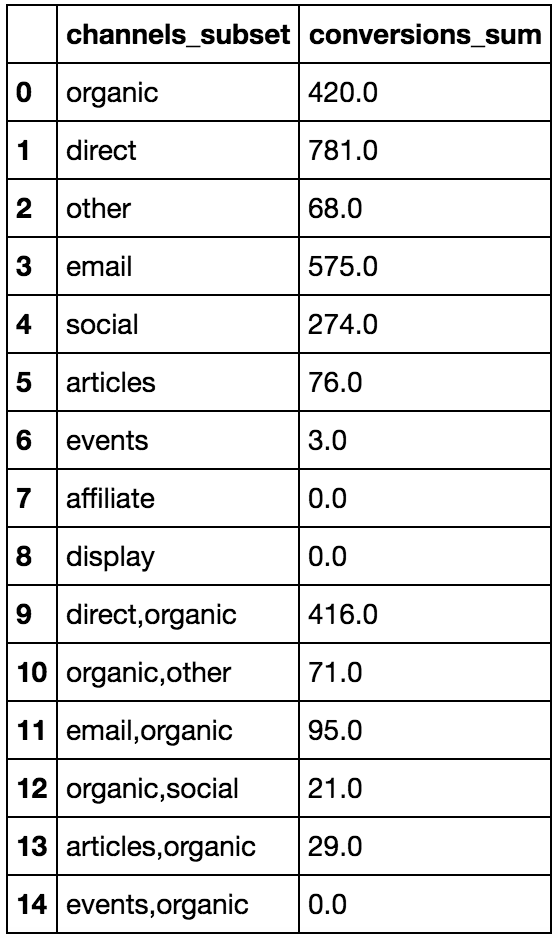
Then, we need to sum these values for each coalition A, using the previous definition of the characteristic function v. The following Python function computes the worth of each coalition A of N by summing the number of conversions of each of its subsets:
def v_function(A,C_values):
'''
This function computes the worth of each coalition.
inputs:
- A : a coalition of channels.
- C_values : A dictionnary containing the number of conversions that each subset of channels has yielded.
'''
subsets_of_A = subsets(A.split(","))
worth_of_A=0
for subset in subsets_of_A:
if subset in C_values:
worth_of_A += C_values[subset]
return worth_of_A
In the above script, subsets is a function that returns for each coalition A, all the subsets that it contains ( for example, if A={a,b,c}, then the function would return the list [{a},{b},{c},{ab},{ac},{bc},{abc}]).
The following Python script applies the above defined function to all the possible coalitions that can be formed:
# First, let's convert the dataframe "subsets_conversions" into a dictionnary
C_values = user_logs_aggr.set_index("channels").to_dict()["conversions"]
#For each possible combination of channels A, we compute the total number of conversions yielded by every subset of A.
# Example : if A = {c1,c2}, then v(A) = C({c1}) + C({c2}) + C({c1,c2})
v_values = {}
for A in subsets(channels):
v_values[A] = v_function(A,C_values)
Once we have all the values that the characteristic function v takes over all possible coalitions, we can compute the Shapley value for each channel. The following Python script implements the Shapley equation:
from collections import defaultdict
n=len(channels)
shapley_values = defaultdict(int)
for channel in channels:
for A in v_values.keys():
if channel not in A.split(","):
cardinal_A=len(A.split(","))
A_with_channel = A.split(",")
A_with_channel.append(channel)
A_with_channel=",".join(sorted(A_with_channel))
shapley_values[channel] += (v_values[A_with_channel]-v_values[A])*(factorial(cardinal_A)*factorial(n-cardinal_A-1)/factorial(n))
# Add the term corresponding to the empty set
shapley_values[channel]+= v_values[channel]/n
The resulting values could look something like the following:

Conclusion
There are two nice properties that come along with this attribution model:
- The first one is that the value of each channel’s attribution is equal to the number of conversions it is accountable for, and that the sum of all the channels’ attributions equals to the total number of conversions that were recorded. This is called the efficiency property.
- The second one is that this approach guarantees that each channel will be accountable for at least the number of conversions that this channel can manage to generate by itself. This is called the individual rationality property.
(You can verify that these two properties hold for the example that we addressed earlier.)
All of the things we have done so far assume that we have the right data under the right format. This requires, among other things, that the user sessions be constructed and well-defined.