This is a blog post from our friends at Morgan Hill and Pine Tree. Morgan Hill is a team comprising ex-CIO’s of multinational businesses, finance professionals, hedge fund managers, data analysts, data scientists, and systems architects, with hundreds of years of experience in delivering solutions to financial markets and to industry, both using advanced algorithm-based technology. Pine Tree is a multi-award-winning quantitative hedge fund that regularly tops all performance league tables, especially in difficult market conditions.
In this blog post, you’ll discover how financial modeling evolved over the years to cope with the concept of fat tails and extreme events and how increasingly complex financial models evolved to require increasingly sophisticated data science models.
Tail risk, or the risk of extreme market scenarios, is not an old concept in finance — not that there haven’t always been extreme events in the markets. Wikipedia currently lists 61 events categorized as “stock market crashes,” dating from the Bengal Bubble of 1769 to the 2020 stock market crash. That equates to, roughly, one every four years or so.
But then, at one point, mathematics came along. From Harry Markowitz in the 1950s to Fischer Black, Myron Scholes, and Robert Merton in the 1960s, mathematicians came up with a series of beautiful theories describing the markets in terms of normal random variables, or diffusion processes.
We already knew a lot about normal random variables and diffusion processes from various branches of mathematics and physics, so the resulting theories were sensible, beautiful, and they seemed to work. Markowitz, Black, Scholes, and Merton were all awarded Nobel prizes for this work.
The Era of Black Swans
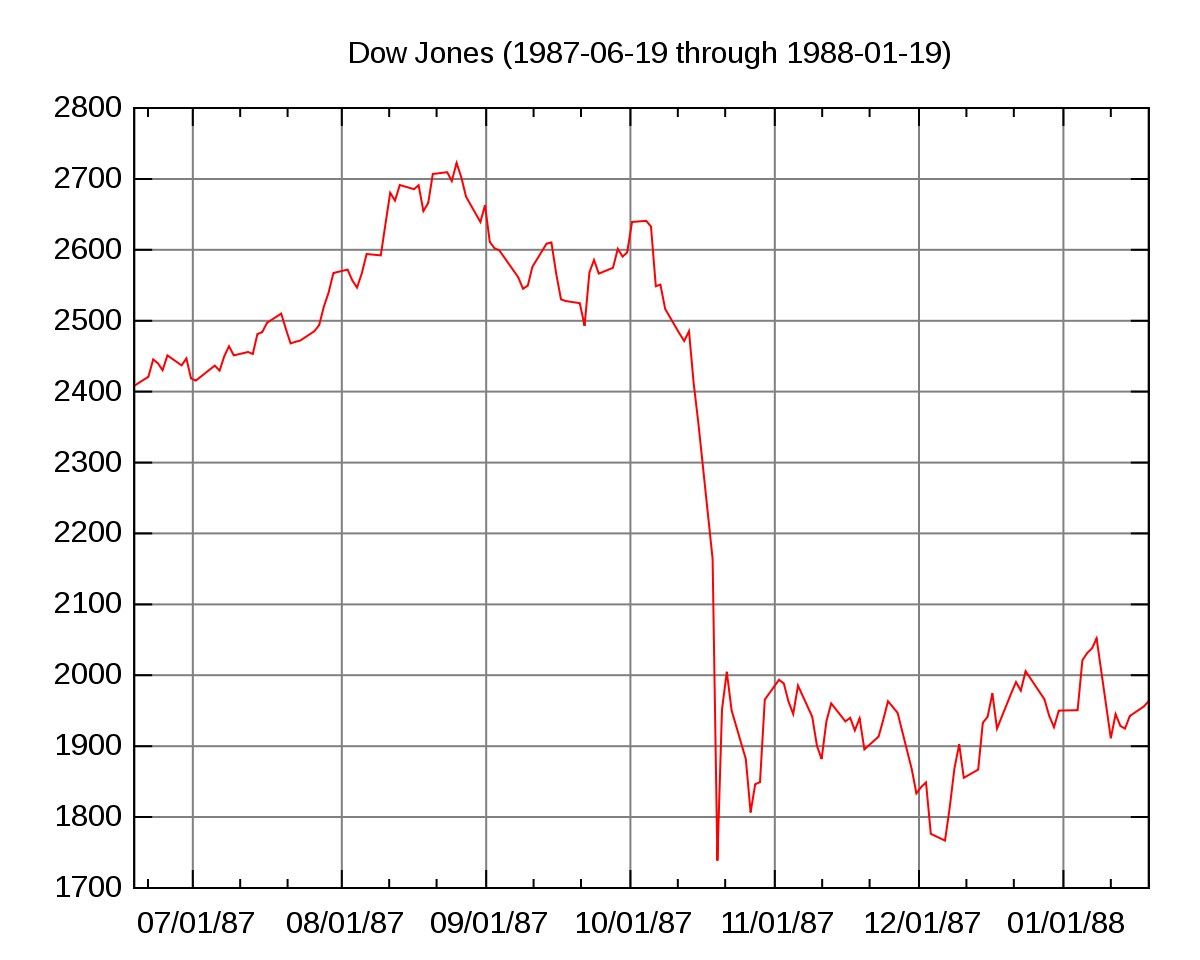
And then, reality came along, in the form of The Black Monday of 1987. Seemingly just another stock market crash — nothing new under the sun. But, something interesting happened in the option markets afterwards. Option traders started to add the so-called volatility smile to their pricing models. Apparently, they no longer trusted that stocks behaved like normal random variables. They needed a hack to price in a realistic probability of extreme events, and it came in the shape of the volatility smile. And it was only a hack. They kept the existing normal models, and they only let the volatility parameter change depending on the price level. A minor change, but now they could price options based on realistic price paths. And those price paths had fat tails.
A few decades later, in 2007, a former option trader by the name of Nassim Taleb published a popular finance book called “Black Swan: The Impact of The Highly Improbable,” where he argued that normal random variables are insufficient to describe the reality of the markets and various rare events, which he called Black Swans. The book became an instant global bestseller, partly helped by the fact that it came out on the eve of the global financial crisis of 2007-2009. And, yet, the world of finance met it with derision. Not because Taleb’s thesis was revolutionary — quite the opposite. The typical reaction was along the lines of “Where has this guy been for the last twenty years?”
From Options to Portfolios
And, yet, these insights from the option markets never quite made it into portfolio management. By the time of the global financial crisis, the state-of-the-art in portfolio construction was still Harry Markowitz’s Modern Portfolio Theory (MPT) from 1952, which is squarely based on normal random variables. The MPT method of portfolio construction is very simple. It consists of three steps:
- Perform Principal Component Analysis (PCA) on the investment universe.
- Normalize each Principal Component (PC) to unit volatility.
- Allocate each PC in proportion to its Sharpe ratio.
Interestingly, Markowitz apparently did not follow his own recipe when it came to investing his own money. It has been reported that he instead put half of it in equities, and the other half in bonds. Why?
Well, the problem is that each of the above steps only really works if the stock universe indeed follows a multivariate normal random process. If it doesn’t, then it all falls apart. PCs, volatilities, and Sharpe ratios are unsteady, so different observation buckets will give different answers. They describe the past, but, as all investment literature points out, the past is not a reliable guide to the future.
Not that nobody noticed that — quite the opposite. People have tried a number of hacks similar to the volatility smile, with varying degrees of success. From “Hierarchical PCA”, which constrains the PCs so that they couldn’t move much, to the “Principal Eigenportfolio”, which considers only the first PC, which is the only relatively stable one.
Solution
We have, on the other hand, had some successes with a different approach, based on directly penalizing the portfolio for its tail risk. In a forthcoming Risk Magazine paper, we show that by penalizing for kurtosis, or “fat-tailedness” of the portfolio, we get more stable, more diversified portfolios with a lower degree of tail risk. Markowitz’s MPT recipe only changes slightly, in the sense that one has to use Independent Component Analysis (ICA) instead of the PCA, and weight the resulting components by the Fat-tailed Ratio (the ratio of the return to the kurtosis, all to the power of 1/3), instead of weighing them by the Sharpe ratio (the ratio of return to volatility).
So why stop there? Variance and kurtosis are the second and the fourth moment of a distribution — why should we worry specifically about the second and the fourth moment? What is so special about numbers two and four?
As it turns out, nothing. In a paper that just came out in Wilmott, we showed that one can (and should) indeed use moments of any order. This is not a simple task. At the level of decomposition, PCA is no longer sufficient, and the use of ICA is coming under increasing strain. The decomposition required at this level is the kernel PCA, and, in some cases, neural network decomposition.
Insights
Does all that effort pay off in the end? Well, as we gain the ability to set the penalty order at will, interesting things start to happen. For the second order, corresponding to Markowitz’ Modern Portfolio Theory, components are allocated in proportion to their return. Something with twice the return will, all other things being equal, get twice the allocation.
This phenomenon even has a name: “Winner takes all.” It is a recognized problem where a handful of symbols with high return receive a lion’s share of the allocation in a portfolio, at the expense of diversification. And, then, when these high performers stop performing, there is no diversification to fall back on, and the entire portfolio collapses.
Using our approach, though, as we increase the order of the penalty moment, high performers get lower allocations, low performers get higher allocations, and the portfolios get more diversified. It is even possible to take the limit of the penalty order going to infinity, where the allocation becomes a step function. If its return exceeds a hurdle, the component receives a fixed allocation; otherwise, it receives nothing.
The resulting portfolio is perfectly diversified, and that is what provides the best protection against tail risk. This is actually a well-known, ancient trading heuristic which trading desks have been using intuitively for decades — perhaps centuries. Only now, we know why. And we can do it a bit more scientifically, with actual, you know, numbers. It’s also what Harry Markowitz reportedly did with his own money when he put half of it in equities, half in bonds.
More details can be found in the full text references below:
Rosenzweig (2022) Power-law Portfolios. Wilmott 117, pp 50-56.
Rosenzweig (2021) Fat-tailed Factors. Risk (to appear).




