Quantum Machine Learning (QML) leverages quantum computing to solve challenging ML problems that classical computers cannot efficiently handle. Significant advantages are expected for classically-intractable problems, such as searching a very high dimensional space, as required in drug discovery or extracting properties from large graphs with applications in DNA sequencing.
Another aspect of QML explores the reverse approach, exploiting ML techniques to improve quantum error-correction, estimate the properties of quantum systems, or develop new quantum algorithms.
This article gives an overview of how quantum computing could accelerate ML, offering the prospect of more efficient training for extensive models, such as large language models (LLMs). This concludes our three-part series on technical subjects that have gained attention due to the increasing interest for LLMs (see first and second articles of the series).
Quantum Bits and Circuits
Quantum computers do not process classical bits, but quantum bits, or Qubits, which have larger representative power than bits. Qubits don’t have a deterministic binary state, either 0 or 1, but a Quantum State, where they can be in both the possible states: 0 with contribution α and 1 with contribution β, where α² and β² represent the probability of measuring a state of 0 or 1 respectively (α²+β²=1).
The state of one qubit is thus defined by two numbers; similarly, the state of two qubits is defined by four numbers (one per each possible state 00, 01, 10, 11), so that the amount of equivalent information contained in N qubits is 2ᴺ classical bits. This is just an intuition of why qubits can store more information than classical bits, but for the exact explanation, have a look at these video lectures.
We can consider a quantum state as a generalization of classical probability distribution and quantum computation is a way to transform these probability distributions. As for bits, logical operations can be defined on qubits and make up Quantum Circuits that can also implement ML models.
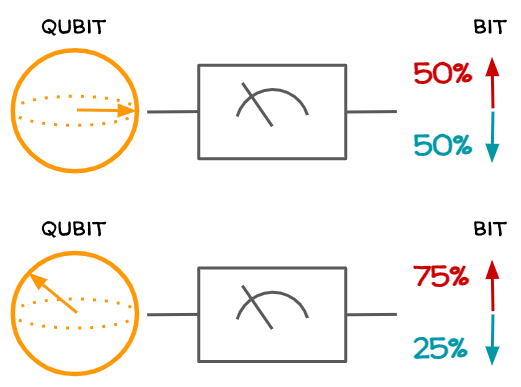
The outcomes of quantum systems are defined by quantum states and are thus probabilistic. In order to retrieve an observable result from the system, we need to measure the qubit, which makes it collapse to a deterministic value of 0 or 1, with probability depending on its state before measuring (see figure below).
Although there is no standard yet for the physical implementation of qubits (electron’s spin, nuclear spin, polarization of a photon and others have been used), the most common approach today, adopted by Google and IBM to build their Quantum Computers, is superconducting qubits.
Quantum Computers as AI Accelerators
Quantum Processing Units (QPU) do not outperform classical computers universally in terms of speed for every operation. However, for specific types of algorithms, quantum computers can achieve results with exponentially fewer operations compared to their classical counterparts.
This is the case for the Shor’s algorithm to find prime factors of an integer, which has been proven to be so fast that it could break the widely used RSA encryption protocol. But this is a theoretical result based on ideal, universal quantum computers, which are still years away.
The biggest challenge in scaling up quantum computers is dealing with noise that can arise from various environmental interferences (thermal fluctuations, imperfections in quantum gates, etc.) and that affect the state of qubits causing information loss. Fault-tolerant devices employ error correction schemes that are very challenging to implement, as they can introduce new sources of errors.
For practical applications, the latest QML research focuses on near-term quantum devices, called Noisy Intermediate-Scale Quantum (NISQ) processors. NISQs typically comprise approximately 1,000 qubits, but they have not reached the level of advancement to support fault-tolerance or attained the necessary size for realizing theoretical quantum speedups (for comparison breaking RSA encryption would require 20 M qubits).
These quantum devices can be seen as special-purpose hardware, with several AI companies offering simulators for testing or cloud services for real-world deployment:
- Google offers a Quantum Virtual Machine with simulators up to 40 qubits. They plan to provide for research their 53-qubits Sycamore processor, the first to be claimed to achieve quantum supremacy for its ability to solve a problem faster than any classical computer can feasibly do, in the controversial 2019 Nature paper, contested by IBM.
- IBM provides a Quantum Platform (up to 133 qubits) and owns the largest quantum device on earth, the Condor with more than 1,000 qubits, and is planning to develop a 100,000 qubits device in 10 years,
- Pure quantum companies: Xanadu (up to 216 qubits), Rigetti (up to 84 qubits),
- Microsoft Azure Quantum, and Amazon Braket are distributing devices from other providers.
Encoding Classical Data Into Quantum Data
Quantum circuits, even those implementing ML models, are not meant to work on classical data, such as images or text. They’re designed to process Quantum Data, that is any data that emerges from an underlying quantum mechanical process, such as some properties of molecules, or data generated by a quantum device (some examples here).
In order to apply QML algorithms to classical data, the data must first be reformulated into quantum states via quantum-embedding, specifying circuits that generate the data. This step is pivotal as it impacts the computational power of the algorithm, and there is ongoing discussion about its scalability [2]. Investigating the optimal quantum embedding strategies is an active area of research.
First Generation Quantum ML
Quantum computers have the ability to perform fast linear algebra on a state space that grows exponentially with the number of qubits. The first generation of QML algorithms leverage this quantum accelerated linear-algebra to solve unsupervised and supervised learning tasks:
- Grover’s algorithm can offer quadratic speedup for any search process, thus accelerating k-means, k-NN, training perceptrons and computing attention in LLMs [15].
- HHL (Harrow–Hassidim–Lloyd) algorithm offers quadratic speedup for doing matrix inversion, thus accelerating support vector machines (SVM), principal component analysis (PCA) and recommendation systems.
Like for the Shor’s algorithm, the above speedup is a theoretical result on certain types of quantum data and will only have practical validity on future generations of quantum hardware.
Moreover, many common approaches for applying these algorithms to classical data rely on encoding data into inherently more efficient structures that can also be exploited by classical algorithms. This has led to the emergence of another category of fast algorithms, called Quantum-Inspired, with the same assumptions as quantum algorithms but executable on classical hardware.
Second Generation Quantum ML
Similar to how ML progressed into deep learning with the advent of enhanced computational capabilities, QML is also transitioning towards heuristic methods, facilitated by the accessibility and advancements in quantum hardware for empirical study.
These new QML algorithms use parameterized quantum transformations called Parameterized Quantum Circuits (PQCs) or Quantum Neural Networks (QNNs). Like in classical deep learning, the parameters of these models are optimized with respect to a cost function via either black-box optimization heuristics or gradient-based methods.
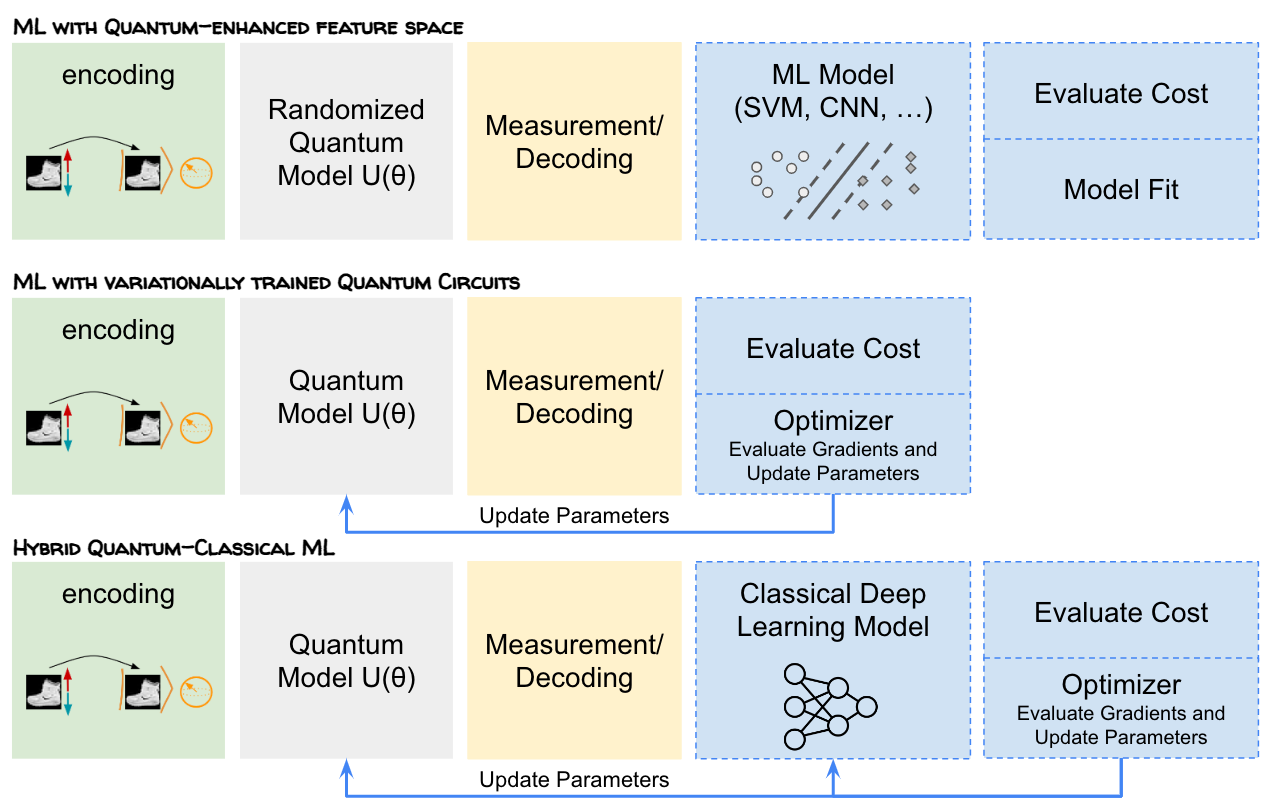
The most popular approaches to QML today are hybrid (figure below) and can be classified into the next three categories.
ML With Quantum-Enhanced Feature Space: Quantum circuits are used to extract features and their parameters are not learned. It consists of three steps:
- 1. Data encoding to quantum space.
- 2. PQC with randomized parameters used to generate features (for instance as convolutional filters [8] or kernel functions [9]).
- 3.Extraction of classical information via measurements and post-processing it in a classical ML framework (i.e. linear SVM [9]).
These techniques extract features via a combination of random nonlinear functions of the input data, which is an approach already used in classical ML to approximate complex models [9]. What QML brings on the table is the ability of generating more complex random nonlinear functions, hard to simulate on classical computers, enabling more expressive features and higher performance. Most existing applications focus on image classification, but the same methods are also extended to NLP, time series forecasting, customer segmentation and others.
ML With Variationally Trained Quantum Circuits: Here, the parameters of PQC are updated as part of the training process [10, 11]. Variational training refers to the fact that the parameters to be learned are parameters of probability distributions (like for Variational Auto Encoders). In this approach, classical computers are used as outer-loop optimizers for PQCs.
One significant challenge in training such quantum models is referred to as barren plateaus [12], which represent a flat loss landscape that increases with the number of qubits, impeding the effectiveness of optimization techniques. Additionally, the current noise level in quantum devices imposes limitations on the achievable depth of quantum circuits with acceptable fidelity. These factors drive the motivation for the next hybrid approach, aiming to retain as much of the model as feasible on classical hardware.
Hybrid Quantum-Classical ML: Here, the model itself is a hybrid between quantum computational building blocks and classical computational building blocks and is trained typically via gradient-based methods.
There are two main python open source libraries to implement QML:
- Pennylane with its rich gallery of demos. This library is well-integrated with the most used software to implement and run quantum circuits (IBM’s Qiskit, Google’s Cirq, Rigetti’s Forest, or Xanadu’s Strawberry Fields) and has interfaces to the most popular automatic differentiation libraries (NumPy, PyTorch, JAX, and TensorFlow)
- Google TensorFlow Quantum for Hybrid Quantum-Classical ML (integrating Cirq with TensorFlow)
Quantum Kernels
Over the last few years, research in QML has offered valuable insights into the close connection between the mathematical foundation of quantum circuits and so-called kernel methods, the most famous of which is the support vector machine (SVM) [3].
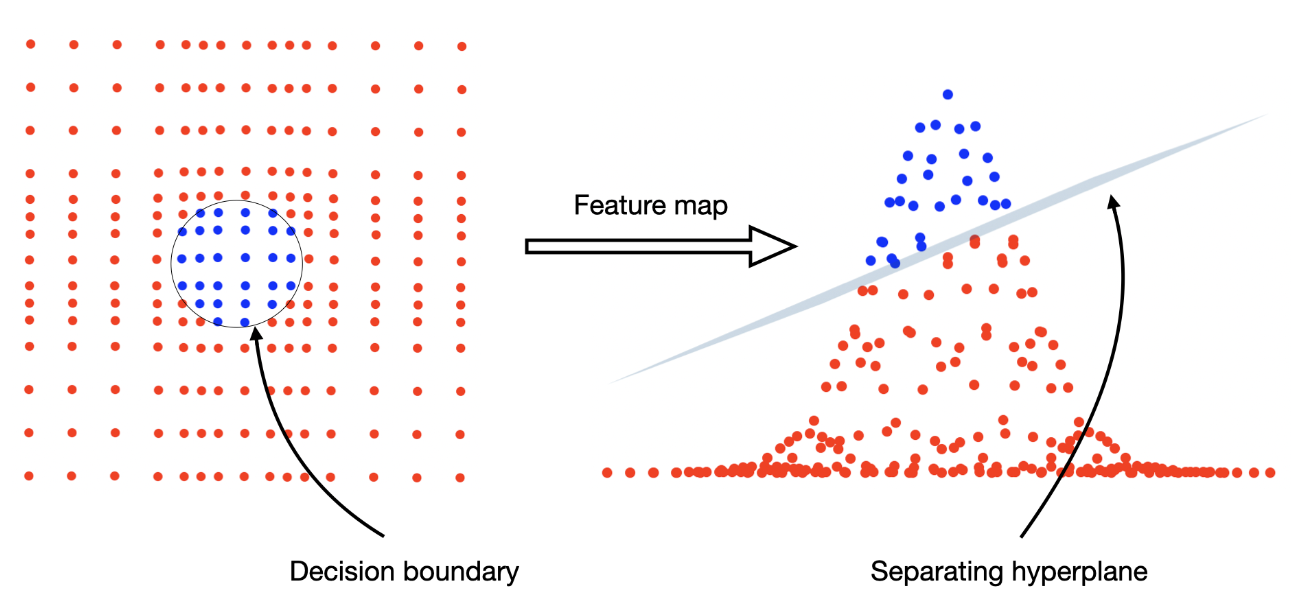
Kernel methods consist in defining kernel functions mapping data into underlying higher dimensional space, where the data is easier to classify (see figure below). For data encoded in quantum circuits, we can define kernel functions that prove challenging or impossible to replicate on classical computers, and that can perform better for some tasks.
In the quantum-enhanced approach, Quantum Kernels are used to define a new feature space to be then used with a classical linear SVM for instance, in a way similar to what is done in traditional ML. What’s new in QML is the possibility to define trainable kernels in the variationally trained approach, where the quantum kernels are learnt by optimizing a cost via gradient based techniques (see this pennylane tutorial).
In 2021, IBM researchers [7] proved an exponential speed advantage of trained quantum kernels over classic ones for certain classes of classification problems. Their quantum kernel method identifies the pertinent features for classification within a specifically designed family of datasets. These datasets possess intrinsic labeling patterns recognizable only by quantum computers, whereas for classical computers, the dataset appears as random noise.
Initial findings in QML research suggest that the advent of larger, fault-tolerant quantum computers is likely to reduce the quadratic scaling of kernel methods to linear scaling. This potential advancement could position classical as well as quantum kernel methods as robust alternatives to neural networks for processing big data [3].
What Is Still Missing?
While tests analyzing the structure of a dataset have been designed to assess the possibility of a quantum speedup on that specific task [14], it is not yet proven that QML can provide a speedup on practical classical ML applications.
A critical focus of research is the improvement of encoding techniques of classical data into the quantum space, but also more generally understanding if there are certain types of data that are best structural fits for quantum circuits.
Other research questions in QML regard the improvement of training techniques, and the definition of better loss functions and performance metrics. Using classical ML benchmarking is considered detrimental to the field of QML, for which understanding the best scope and usability is still to come. QML should not be seen in competition with machine learning, but rather as a new way to boost it.
[1] The Emerging Role of Quantum Computing in Machine Learning (Henderson, 2020)
[2] TensorFlow Quantum: A Software Framework for Quantum Machine Learning (Broughton et al., 2021)
[3] Supervised quantum machine learning models are kernel methods (Schuld, 2021)
[4] How does a quantum computer work ? (2013)
[5] Quantum Machine Learning: What is still missing? (Schuld, 2023)
[6] A rigorous and robust quantum speed-up in supervised machine learning (Liu et al., 2021)
[7] Quantum kernels can solve machine learning problems that are hard for all classical methods (2021)
[8] Quantvolutional Neural Networks (Henderson, 2019)
[9] Quantum Kitchen Sinks (Wilson, 2019)
[10] Quantum circuit learning (Mitarai, 2018)
[11] Supervised learning with quantum enhanced feature spaces (Havlicek et al., 2018)
[12] Barren plateaus in quantum neural network training landscapes (McClean et al., 2018)
[14] Power of data in quantum machine learning (Huang et al., 2022)
[15] Fast Quantum Algorithm for Attention Computation (Gao et al., 2023)




